Can I rely on PHP php.ini precision workaround for floating point issue

Question

I've found some workaround for floating point problem in PHP:

php.ini setting precision = 14

342349.23 - 341765.07 = 584.15999999992 // floating point problem

php.ini setting, let's say precision = 8

342349.23 - 341765.07 = 584.16 // voila!

Demo: http://codepad.org/r7o086sS

How bad is that?

1. Can I rely on this solution if I need just precise 2 digits calculations (money)?

2. If not can you provide me a clear example when this solutions fails?

Edit: 3. Which php.ini.precision value suits best two digits, money calculations

---

• Please mind I can't use integer calculations (float*100 = cents), it's far too late for that.
• I am not going to work on numbers higher than 10^6
• I don't need to compare numbers

UPDATE

@Baba answer is good, but he used precision=20, precision=6 in his tests... So still i am not sure is it gonna work or not.

Please consider following:

Let's say precision = 8 and only thing I do is addition + and subtraction -

A + B = C

A - B = C

Question 1: Is precision workaround gonna fail for numbers between 0..999999.99, where A and B is a number with decimal places? If so please provide me an example.

Simple test would do the job:

// if it fails what if I use 9,10,11 ???
// **how to find when it fails??? **
ini_set('precision', 8); 
for($a=0;$a<999999.99;$a+=0.01) {
  for($b=0;$b<999999.99;$b+=0.01) {
     // mind I don't need to test comparision (round($a-$b,2) == ($a-$b))
     echo ($a + $b).','.($a - $b)." vs ";
     echo round($a + $b, 2).','.round($a - $b, 2)."
";
  }
}

but obviously 99999999 * 2 is too big job so I can't run this test

Question 2: How to estimate/calculate when precision workaround fails? Without such crazy tests? Is there any mathematicial*, straight answer for it? How to calculate is gonna to fail or not?

*i don't need to know floating point calculations works, but when workaround fails if you know precision, and range of A and B

---

Please mind I really know cents and bcmath are best solution. But still I am not sure is workaround gonna fails or not for substraction and addition

Answer 1

Introduction

Floating-point arithmetic is considered an esoteric subject by many people. This is rather surprising because floating-point is ubiquitous in computer systems. Most fractional numbers don't have an exact representation as a binary fraction, so there is some rounding going on. A good start is What Every Computer Scientist Should Know About Floating-Point Arithmetic

Questions

Question 1

Can I rely on this solution if I need just precise 2 digits calculations (money)?

Answer 1

If you need need precise 2 digits then the answer is NO you can not use the php precision settings to ascertain a 2 digit decimal all the time even if you are not going to work on numbers higher than 10^6.

During calculations there is possibility that the precision length can be increased if the length is less than 8

Question 2

If not can you provide me a clear example when this solutions fails?

Answer 2

ini_set('precision', 8); // your precision
$a =  5.88 ; // cost of 1kg
$q = 2.49 ;// User buys 2.49 kg
$b = $a * 0.01 ; // 10% Discount only on first kg ;
echo ($a * $q) - $b;

Output

14.5824 <---- not precise 2 digits calculations even if precision is 8

Question 3

Which php.ini.precision value suits best two digits, money calculations?

Answer 3

Precision and Money calculation are 2 different things ... it's not a good idea to use PHP precision for as a base for your financial calculations or floating point length

Simple Test

Lest Run some example together using bcmath , number_format and simple minus

Base

$a = 342349.23;
$b = 341765.07;

Example A

ini_set('precision', 20); // set to 20 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

Output

584.15999999997438863
584.15999999999996817    <----- Round having a party 
584.16
584.15  <-------- here is 15 because precision value is 20

Example B

ini_set('precision', 14); // change to  14 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

Output

584.15999999997
584.16
584.16
584.16  <-------- at 14 it changed to 16

Example C

ini_set('precision', 6); // change to  6 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

Output

584.16
584.16
584.16
584.00  <--- at 6 it changed to 00 

Example D

ini_set('precision', 3); // change to 3
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

Output?

584
584
584.16   <-------------------------------- They only consistent value 
0.00 ?<--- at 3 .. everything is gone 

Conclusion

Forget about floating point and just calculate in cents then later divided by 100 if that is too late just simply use number_format it looks consistent to me .

Update

Question 1: Is precision workaround gonna fail for numbers between 0..999999.99, where A and B is a number with decimal places? If so please provide me an example

Form 0 to 999999.99 at increment of of 0.01 is about 99,999,999 the combination possibility of your loop is 9,999,999,800,000,000 I really don't think anyone would want to run such test for you.

Since floating point are binary numbers with finite precision trying to set precision would have limited effect to ensure accuracy Here is a simple test :

ini_set('precision', 8);

$a = 0.19;
$b = 0.16;
$c = 0.01;
$d = 0.01;
$e = 0.01;
$f = 0.01;
$g = 0.01;

$h = $a + $b + $c + $d + $e + $f + $g;

echo "Total: " , $h , PHP_EOL;


$i = $h-$a;
$i = $i-$b;
$i = $i-$c;
$i = $i-$d;
$i = $i-$e;
$i = $i-$f;
$i = $i-$g;

echo $i , PHP_EOL;

Output

Total: 0.4
1.0408341E-17     <--- am sure you would expect 0.00 here ;

Try

echo round($i,2) , PHP_EOL;
echo number_format($i,2) , PHP_EOL;

Output

0
0.00    <------ still confirms number_format is most accurate to maintain 2 digit 

Question 2: How to estimate/calculate when precision workaround fails? Without such crazy tests? Is there any mathematical*, straight answer for it? How to calculate is gonna to fail or not?

The fact sill remains Floating Point have Accuracy Problems but for mathematical solutions you can look at

• Machine precision and backward error analysis
• Minimizing the effect of accuracy problems

i don't need to know floating point calculations works, but when workaround fails if you know precision, and range of A and B

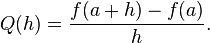
Not sure what that statement means :)